A classical approach for modeling the dynamical behavior of mechanical systems is based on variational principles, e.g. Hamilton’s principle, which leads to the Euler-Lagrange equations.
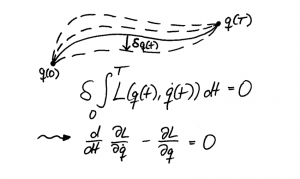
However, computational methods require a time-discrete representation of the system dynamics. Discrete mechanics can be obtained by a discretization of the variational principles. This leads to a class of integration schemes — so called variational integrators — which are naturally structure-preserving, i.e. they preserve symmetry (invariances) and symplecticity (area-preservation) and have an excellent long-time energy behavior. Recent work has extended variational integrators to hybrid, constrained, or stochastic mechanical systems, as well as to electrical systems, for instance.

In my PhD thesis, I extended these variational principles to hybrid systems and used the optimal control method DMOC (Discrete Mechanics and Optimal Control) to develop a structure-exploiting motion planning method for mechatronic systems.
Furthermore, discrete mechanics can be used to design structure-preserving feedback regulators which can be used in robotics applications (see NxR Lab Website, for instance).