Hybrid systems are dynamical systems with mixed continuous-time and discrete-time behavior. Hybrid dynamics arise for various reasons: abrupt changes of motions of mechanical systems, for instance, because of impacts, changes in the topology, in mechatronic systems induced by logic devices, triggered by advisory switching controllers, or as a simplification of complex nonlinear behavior. The optimal control of hybrid systems thus require an optimization of continuous and discrete variables.
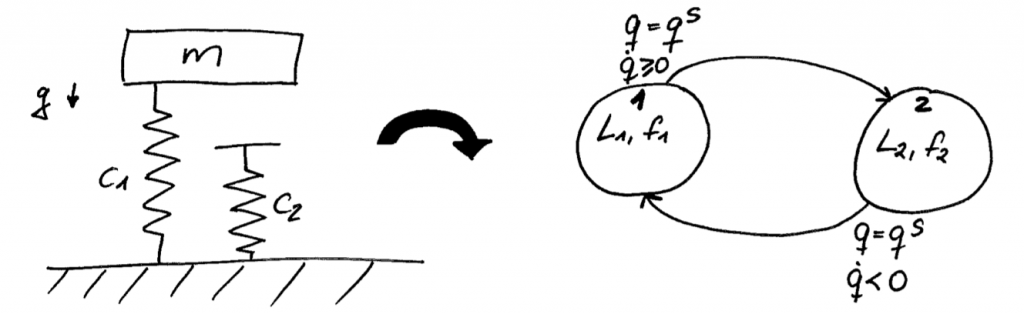
This is an example of a hybrid system with switches state-dependently between two modes, both defined by a Lagrangian, and, possibly, forcing terms (see this paper for details).
I am particularly interested in the optimal control of switched and hybrid mechanical systems. As we showed here, in a discrete-time formulation, a switching time optimization problems turns into a non smooth optimization problem and thus, has to be treated appropriately. Variational integrators can be extended to hybrid mechanical systems, and so, questions of structure-preservation and efficiency in numerical control or estimation algorithms arise again.